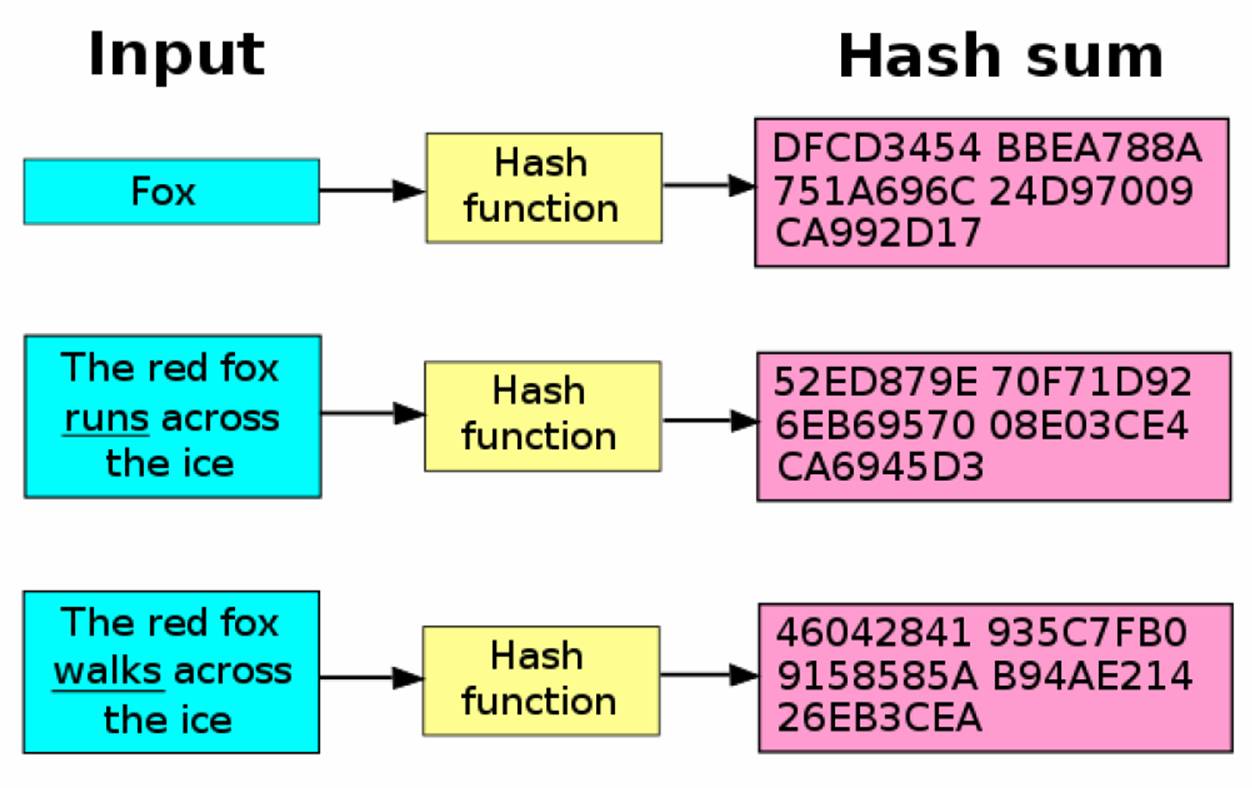
Hashes are a way of taking any amount of data, jumbling it around, then shrinking the result to a fixed-size output, a fingerprint. A cryptographic hash function or algorithm takes in an arbitrary block of data and returns a fixed-length hash, such that any accidental or intentional change to the data will, with very high probability, change the hash value.
When selecting a hashing function we look for two things:
Pre-image Resistance: Trying to figure out a hash’s input when we only know it’s output is known as pre-imaging. We don’t want someone to be able to look at a hash and figure out what input was used to create that hash. That would defeat the whole purpose. An algorithm that’s very easy in the forward direction but extremely difficult in the backward direction is what we’re looking for.
Collision Resistance: A hash reduces an input that may be billions of bits long into a sequence that may be only a few thousand bits long. By definition, this means that we are going to have multiple inputs that lead to the same output, a collision. We want a hash function that is as resistant to collisions as possible, that is, the output should be spread out as evenly as possible over it’s entire range of output combinations.
These two qualities boil down to randomness and sensitivity. The output should appear quite random (note that it can never be a truly random process as hashing is purely deterministic). And two similar inputs should not produce similar hashes. Even if the input differs by just one bit, the output must be vastly different.
What are hashes used for?
Perhaps the most common use of hash functions is in hash tables, a form of data structure (like arrays or trees) that can facilitate rapid data lookup, like the kind needed by Google to index billions of web pages on the internet.
Secondly, a hash can be used as an integrity check for a file. You’ve probably seen file hashes provided alongside downloads, like this:
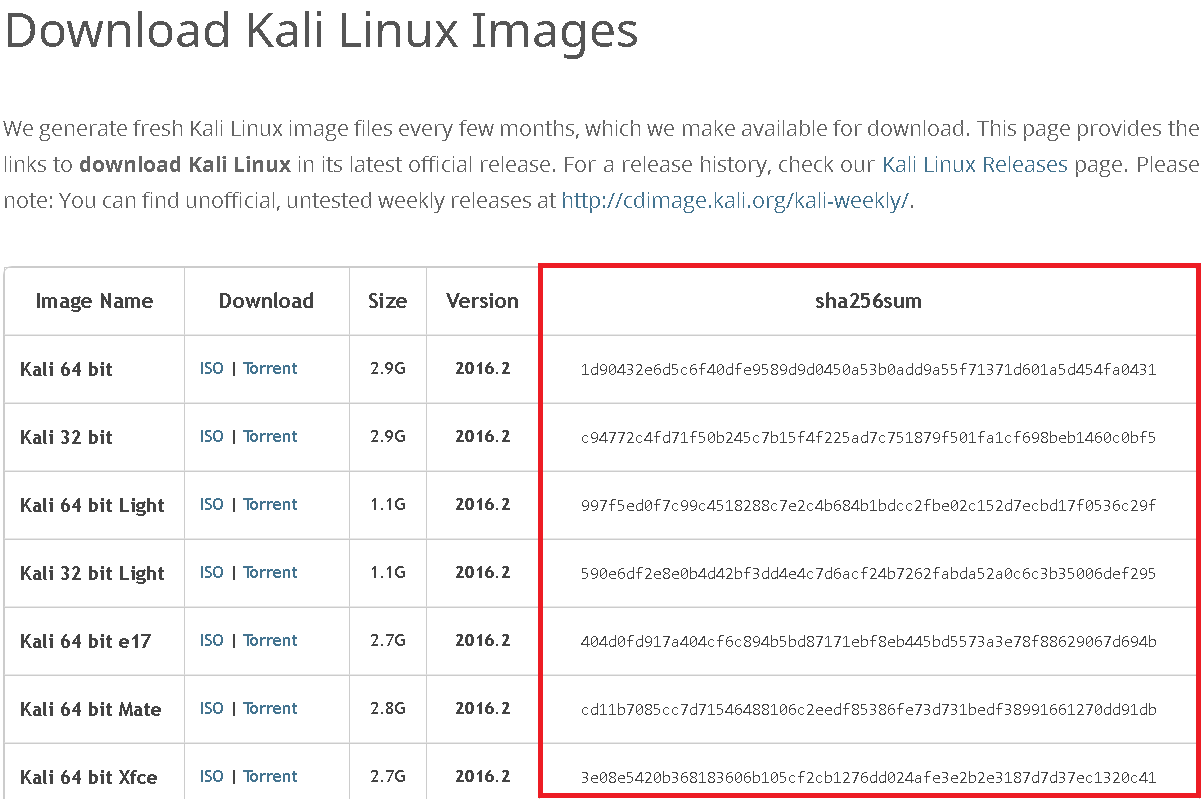
What you see above are the SHA-256 hashes for Kali’s OS images. When you download the image, you can then run the hashing algorithm on the file and if you get the same hash as what’s shown up there, then you can be certain that what you’ve downloaded is the exact same pattern of bits that make up the specific file, since if even a single bit were corrupted, the hash would be something completely different.
What are some popular hashing algorithms?
| Hashing Algorithm | Example |
|---|---|
| MD5 | 8743b52063cd84097a65d1633f5c74f5 |
| SHA1 | b89eaac7e61417341b710b727768294d0e6a277b |
| MD4 | afe04867ec7a3845145579a95f72eca7 |
| SHA256 | 127e6fbfe24a750e72930c220a8e138275656b8e5d8f48a98c3c92df2caba935 |
| SHA512 | 82a9dda829eb7f8ffe9fbe49e45d47d2dad9664fbb7adf72492e3c81ebd3e29134d9bc12212bf83c6840f10e8246b9db54a4859b7ccd0123d86e5872c1e5082f |
Rainbow Tables and Salting
Hash functions are generally pretty strong, however, as always, a brute force attack is a way around the security. You may have heard of things called rainbow tables - these are essentially massive tables of message-digest pairs for a certain algorithm. Indirectly, a trade off between time taking CPU power and memory storage.(Message-Digest pair simply means, in this case, a possible password and the weird string it gives when run through a hashing function)
For example, say a bunch of powerful computers have been working at generating message-digest pairs for an algorithm for a fair amount of time (there are a lot of combinations), and they’ve managed to list all the character combinations and associated hashes for up to 5 characters in message length with a known hashing function. If you’re running a website which simply hashes users passwords in a database with this popular (and presumably secure) algorithm, this means that if your users’ passwords aren’t very complex, they may already be listed in the rainbow table. So if an attacker breaks in, they could simply run all the hashes against the rainbow table, hence getting the original passwords for users with weaker passwords. For example, say your database shows the association user: JBsux; password: 9d4e1e23bd5b72, however an entry for “9d4e1e23bd5b72” is found in the rainbow table through a quick search-through, and the hash is translated back into the original password ,say: “IsecretlyluvJB” and now.. you’re screwed, in more than one way.
This is a pretty big problem - not only can users not really be trusted to come up with secure passwords a lot of the time, but popular algorithms are usually the more secure ones, however this in turn means that more people will be interested in putting their CPU horsepower towards bettering the rainbow tables to break more hashes in that algorithm.
(Note: Rainbow tables are just a method to brute force and they suffer from the same weakness : Exponential growth. While most passwords up to 8 characters can be crammed into a reasonable 4 Terabyte hard disk, take it up to 12 characters and you’re looking at over 10 freaking Exabytes or 10 million Terabytes. Further, I got this figure by using the charset: {A-Z,a-z,0-9} = I didn’t even consider symbols. Count those in and you literally cannot store the possible combinations on every storage device on the planet, combined. Oh and did I mention that it might actually take even a supercomputer possibly hundreds of thousands of years to actually create that much data ? And still, Rainbow tables are viable enough to deserve a mention here and they actually do work, Amazing isn’t it? The main reason being - Weak Passwords. (Surprisingly, “IsecretlyluvJB” at 14 characters long is actually pretty strong and the above example would be technically and practically correct only for a smaller password like “pass”))
Luckily, this problem isn’t too difficult to solve. Generating rainbow tables is only really viable for a certain number of characters as the possible combinations of characters simply gets too high for a rainbow table to be generated for all the combinations practically. So to combat rainbow tables, all we really have to do is add a bunch of characters to the end of the password before we hash it, and we have a totally different hash which won’t be in the rainbow table. These extra characters are called salts. These are usually pretty big, around 10-20 or more characters and protect the naive users who put in a 4 character password. The server may simply append the salt to the user inputted password and then hash it.
There’s one more important precaution that should be taken. Another example: Say, we own a site with millions of users. If we use the same salt for each user password, it’s probably worthwhile for attackers to go out of their way to actually generate a custom rainbow table for values with our salt attached to them! The solution to this is also very simple - use random salts. If salts are different for each user, there’s no way that an attacker can try to get all the passwords in the database, even with a LOT of time and a LOT of storage memory whereas for the server, it can simply store the username and password hash along with the randomly generated salt and use it again when the user enters the password for logging in.
If attackers wanted to target a specific user, of course, they could waste a whole bunch of time trying to generate a rainbow table specifically for that salt, however if the user has a strong password it will simply take too long as there are way too many character combinations that the password could contain.
In conclusion, Hashes are today’s way of encrypting (mostly) passwords. A great invention, they are here to stay for quite a while but like every security system they are flawed. There’s only so much a company and their servers can do to make sure their users are kept safe, in the end it’s up to the users to look out for themselves. The annoying websites which require the passwords to contain say, A capital letter + A number + A symbol, are in fact the most secure. Whereas the ones who accept 4 character length passwords, although convenient are also the most insecure, Hence it’s up to the user to keep themselves safe.
Want to be a real hacker? Sign Up!